반응형
선형 회귀란?
- 종속 변수 y와 한개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀 분석 기법이다. 즉, 최적선(line of best fit)을 찾는 것이 중요하다.
용어 정리
- 목표 변수 (target variable or output variable) : 우리가 맞추려고 하는 값.
- 입력 변수 (input varaible) : 목표 변수를 맞추기 위해서 사용하는 값. ex) 집의 크기(평수)로 가격을 예측하려 한다면, 입력 변수(집 크기), 목표 변수(집 가격)
- 가설 함수 (hypothesis funciton) : 최적선을 찾아내기 위해 다양한 함수를 시도하는데, 시도하는 함수 하나하나를 가설 함수라고 부른다
- 손실 함수 (loss function) : 어떤 가설 함수를 평가하기 위한 함수. 손실 함수의 아웃풋이 작을수록 가설 함수의 손실이 적기 때문에 더 좋은 가설 함수라고 할 수 있고, 반대로 손실 함수의 아웃풋이 클수록 가설 함수의 손실이 큰 거기 때문에 더 나쁜 가설 함수라고 할 수 있다. 즉, 특정 가설 함수의 평균 제곱 오차가 크면 이 손실 함수의 아웃풋이 크다는 거고, 그러면 손실이 크기 때문에 안 좋은 가설 함수라는 것이다. 반대로 가설 함수의 평균 제곱 오차가 작으면 이 손실 함수의 아웃풋이 작다는 거고, 그러면 손실이 적기 때문에 좋은 가설 함수인 것이다. (.J라는 문자로 주로 표현함.)
가설 함수 표현법
집의 가격을 찾아내는 가설 함수를 찾는다고 가정하자. 하지만 사실 생각해 보면 집 가격을 예측하는 데, 집의 크기 말고도 영향을 끼치는 요소가 굉장히 많다. 그걸 다 반영하려면 결국 우리는 입력 변수가 여러 개가 될 것이다.
입력 변수가 많아지면 : 문자가 너무 많아져서 헷갈린다.
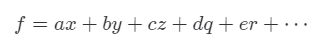
따라서, 좀 더 일관성 있도록 표현하기 위해
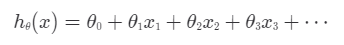
이렇게 표현한다. 선형 회귀의 목적은 가장 적절한 세타 값들을 찾아내는 것이다.
1. 가설 함수 평가법 : 평균 제곱 오차 (MSE. Mean Squared Error)
MSE : 데이터들과 가설 함수가 평균적으로 얼마나 떨어져 있는지 나타내기 위한 하나의 방식. 각 데이터마다 오차를 구한 뒤, 오차를 제곱하고, 제곱한 값들을 모두 더한 것에서 총 데이터 개수 만큼 나눈다.
제곱을 하는 이유는 양수, 음수를 모두 양수로 표현하기 위함과 오차를 더 부각시키기 위해서이다. ( 오차가 커질수록 더 부각됨)
평균 제곱 오차가 작은 것을 찾는 것이 목적.
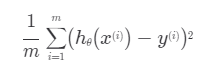
▷ 경사 하강법 (gradient descent)
- 기본 개념 : 함수의 기울기를 구하고 기울기의 절댓값이 낮은 쪽으로 계속 이동시켜 극값에 이를 때 까지 반복시키는 것
- 편미분 개념이 사용된다.
예) 변수가 2개 있을 때.
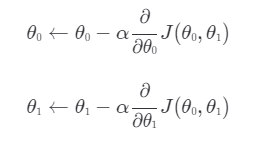
이후 손실 함수 J를 대입한 뒤 편미분 계산을 수행한다.
반응형
'python library' 카테고리의 다른 글
| Pandas (0) | 2021.11.19 |
|---|---|
| Jupyter Notebook 기본 (0) | 2021.11.18 |
| numpy : A matrix Library in python (2차원 배열) (0) | 2021.10.28 |
| numpy 기초(1차원 배열) (0) | 2021.10.28 |
